Introduction

Rapid eye movement (REM) Unique sequence number systems are important in generating random keys. The arithmetic concepts and unique sequences like Prime, Fibonacci, and Lucas numbers are widely used in public-key cryptography because they offer nearly randomness and maintain secrecy [1]. Substantial prime numbers are particularly important for secure key generation in algorithms such as RSA, as well as in enhanced methods like Taher and ElGamal [2,3,4]. Furthermore, Fibonacci numbers have proven useful in many fields, including cryptography, where they facilitate the creation of effective encoding and decoding algorithms. The Fibonacci numbers are potentially enhancing complexity of encoded data [5], and the third-order Fibonacci series significantly enhances the cryptographic characteristics [6].

Lucas sequences boost the efficiency of cryptosystems, particularly in real-time applications, where their repeated computation improves secrecy [7]. When compared to standard binary coding, Lucas Fibonacci sequences offer greater efficiency in symmetric crypto systems. They have demonstrated their effectiveness in securing key distribution [8]. The NS sequence, a type of sum-free sequence, consists of increasing positive integers arranged so that no element can be expressed as the sum of any combination of others [9]. NS sequences are undoubtedly fabricated manually by adding numbers that are not sums of previous elements, but this method is tedious, leading to the development of predefined algorithms for generating large sets. Some NS sets are periodic, while others are proven to be aperiodic [10, 9]. The properties of NS sequences make them strong candidates for cryptographic applications.

With the dawn of powerful quantum computers, the vulnerability of public-key cryptography is becoming more obvious. In contrast, the impact of quantum computers can effectively reduce crypto analysis time by halve for symmetric cryptosystems. This paper introduces enhancement technique for cryptosystem based on the NS sequence, withstanding the powerful quantum computer. Our analysis indicates that this proposed methodology significantly raises the computational resources required for such attacks. This approach addresses the urgent need for security enhancement while also focusing on improving performance digital communication [11]. Elliptic curve cryptography (ECC) and RSA rely on the difficulty of computing discrete logarithms or factoring large numbers—problems that quantum computers can solve efficiently using algorithms like Shor's algorithm [12, 13].

As cryptographic systems confront the looming risk of quantum attacks, global efforts are underway to establish standardized PQC algorithms [11, 14]. Consequently, new mathematical techniques and theories have been developed that extend beyond the realm of PQC and have applications in both computer science and mathematics [15]. One significant area of research is lattice-based cryptography, analyzing the properties and characteristics of these lattices is essential for advancing this field [16]. Managing compatibility with legacy systems is crucial to ensuring the widespread adoption and effectiveness of PQC across various technological environments [17].

Key Contributions

  1. 1.

    The introduction of the No-Sum (NS) sequence, defined as a sequence in which no element can be expressed as the sum of any subset of the set.

  2. 2.

    The development of the RLP (2.0) cryptosystem, which is based on the NS sequence.

  3. 3.

    Use of RLP in Hom orphic Encryption.

  4. 4.

    Demonstrations of security enhancement of symmetric and asymmetric pre-quantum cryptosystem and quantum key distribution mechanism.

The rest of this research is as follows. "Related Works" presents related works. "Post Quantum Crypto System [NIST]" discusses current post quantum cryptography. "Properties of NS Sequences" explores the properties of NS sequence. "Algorithm and Complexity of NS [+−*] Series" illustrates the complexity of NS sequence. "Proposed RLP (2:0) Cryptosystem" Defines RLP (2:0) protocol. "Handshake Process with RLP (2:0)" presents the handshake process with RLP (2:0). "Enhanced AES with RLP (2:0) [24]" presents enhanced AES scheme with RLP (2:0). "Security Analysis: Quantum Attack-Resistant Cryptography Discussion" presents a security analysis. Finally, "Conclusions" concludes the paper and outlines future research directions.

Related Works

The study protocol The National Institute of Standards and Technology (NIST) has initiated a process to standardize post-quantum cryptographic algorithms. This effort includes evaluating various candidates based on their security and performance, with several algorithms selected for standardization in 2022 [18]. Many post-quantum cryptographic schemes are based on lattice problems, which are believed to be hard for quantum computers. Research has shown that lattice-based systems, such as NTRU and learning with errors (LWE), provide strong security guarantees and efficient performance [19]. Multivariate quadratic equations approach involves constructing cryptographic systems based on the difficulty of solving systems of multivariate quadratic equations. These systems have been proposed as candidates for post-quantum cryptography, with ongoing research into their security and efficiency [20]. Code-based cryptographic schemes, such as the McEliece cryptosystem, have been studied extensively. They rely on the hardness of decoding random linear codes, which remains secure against quantum attacks [21, 22].

The emerging area focuses on the use of isogenies between elliptic curves to create secure cryptographic systems. Research has demonstrated that isogeny-based schemes can achieve strong security with relatively small key sizes [23]. Some researchers advocate for hybrid systems that combine classical and post-quantum algorithms to provide security against both classical and quantum attacks. This approach aims to ensure a smoother transition to post-quantum cryptography [24, 25].

While not a direct replacement for traditional cryptography, QKD offers a method for secure key exchange based on the principles of quantum mechanics. Research continues into integrating QKD with post-quantum cryptographic systems [26, 27]. Various studies focus on the security analysis of proposed post-quantum algorithms, assessing their resistance to known attacks and their performance in practical implementations [18, 28]. Research has highlighted the challenges associated with implementing post-quantum cryptographic algorithms in real-world systems, including efficiency, compatibility with existing protocols, and hardware considerations [29, 30]. Ongoing research is exploring new mathematical foundations for post-quantum cryptography, aiming to develop algorithms that are not only secure but also efficient and practical for widespread use [31, 32].

Post Quantum Crypto System [NIST]

The technology of cryptography dates back thousands of years, with some of the earliest evidence found in hieroglyphics carved into the walls of tombs in Greece [33]. While these ancient inscriptions may not have been technically advanced, they exemplify the fundamental principles of cryptography by securely conveying information [34]. The term "cryptography" itself has rich historical roots, originating from the Greek words “kryptos," meaning hidden, and “graphien,” meaning writing [33]. Throughout history, numerous notable figures have employed cryptographic techniques that have significantly influenced pivotal events, which are now part of our educational curriculum. For instance, Julius Caesar developed the substitution cipher for military communications, while Thomas Jefferson created the wheel cipher, consisting of 26 rotating wheels [33]. Both of these methods illustrate the use of cryptography long before the advent of modern technology. The primary purpose of cryptography is to protect privacy and prevent unauthorized access to sensitive data, serving as a crucial component of risk management [35]. This is achieved by transforming readable data into an unreadable format, thus safeguarding the information contained within. Today, cryptography continues to thrive, supporting various businesses and organizations and driving advancements in information technology systems. Although it was developed thousands of years ago, our current technological landscape would not exist without the ongoing evolution of cryptographic methods [36].

Looking ahead, the future of cryptography is undeniably significant. With new technological developments emerging daily, it is essential to secure these innovations and the data they contain [35]. The National Institute of Standards and Technology (NIST) has introduced three new post-quantum cryptography standards to guide organizations and businesses in this endeavor [37]. These standards represent a vital step toward protecting not only enterprises and their data but also the privacy of users and customers.

There is a Zoo of private and public key cryptography. CRYSTALS-Kyber, Dilithium, FALCON, and SPHINCS+ four PQC have been adopted by NIST [9]. The first three are lattice based and SPHICS+ is has based crypto systems.

CRYSTALS-Kyber is designed for general encryption applications and offers several advantages. It enables two parties to exchange relatively small encryption keys while maintaining efficient operational speeds. Notably, it performs quickly across various platforms and is engineered for efficient, constant-time implementation, utilizing optimized routines consistently across all parameter sets.

Crystal Kyber is a post-quantum key encapsulation mechanism rooted in lattice-based cryptography. According to [38], Kyber’s security relies on the difficulty of solving the module learning with errors (MLWE) problem. The primary goals of Crystal Kyber are to provide small key sizes, accelerate operations, and ensure compatibility with existing infrastructure. However, these advantages come with certain drawbacks. While the implementation speed is beneficial, it also presents opportunities for exploitation. Additionally, Crystal Kyber is susceptible to timing attacks and vulnerable to fault injections, which can compromise its security. Detailed understanding is provided in papers related to Crystals-Kyber [38, 39]. Most simplified Crystle-Kyber is presented and done some comprehensive survey of PQC [34].

Dilithium is a lattice-based signature scheme known for its efficiency and strong security guarantees. It offers good performance in generating and verifying signatures, making it suitable for a wide range of applications.

Falcon is another lattice-based signature algorithm that focuses on small signature sizes and fast verification times. It is particularly designed for use in constrained environments, where efficiency is crucial.

Sphincs+ is a stateless hash-based signature scheme that provides strong security by relying on the properties of hash functions. It is notable for its resistance to quantum attacks, though it typically results in larger signature sizes compared to the lattice-based schemes.

Properties of NS Sequences

These functions are completely predictable. They always generate the same outcome for a given input, independent of the context or system state. Deterministic functions are like well-behaved citizens, adhering to rigid rules without deviating. Deterministic algorithms offer accurate answers for issues. They are dependable and consistent.

Non-Deterministic Functions

These abilities are a little more experimental. When you call them the same input, they may yield distinct outputs for a variety of reasons: non-deterministic algorithms may use random occurrences or decisions. Consider them the mathematical equivalent of wild cards.

Non-deterministic algorithms can explore several pathways concurrently. Imagine they make a quantum jump and exist in numerous states at the same time.

Non-deterministic algorithms cannot solve problems effectively in polynomial time and are unable to predict the next step.

No-Sum sequencie [ +] = NS [P].

Rule 1: Only a random positive integer is used as a starting element of the sequence.

Rule 2: Each new number in the sequence must not be derived by adding any previous or group elements.

Rule 3: Any element must be used for only one instance of any operation.

Figure 1 shows the behavior of NS [+] sequence.

Fig. 1
figure 1

Time required to generate NS (+) sequence

Full size image

No-Sum sequencie [+ , −] = NS[NP].

Rule 1: Only a random positive integer is used as a starting element of the sequence.

Rule 2: Each new number in the sequence must not be derived by adding or subtracting any previous element or group of elements.

Rule 3: Any element must be used for only one instance of any operation.

Figure 2 shows the behavior of NS [+ −] sequence.

Fig. 2
figure 2

Time required to generate NS (+−) sequence

Full size image

No-Sum [+, −, *] = NS [NPP].

Rule 1: Only a random positive integer is used as a starting element of the sequence.

Rule 2: Each new number in the sequence must not be derived by adding, subtracting, or multiplying any previous elements or subgroup of elements.

Rule 3: Each new number in the sequence must not be derived by multiplying any previous elements or group of elements.

Rule 4: Any element must be used for only one instance of any operation.

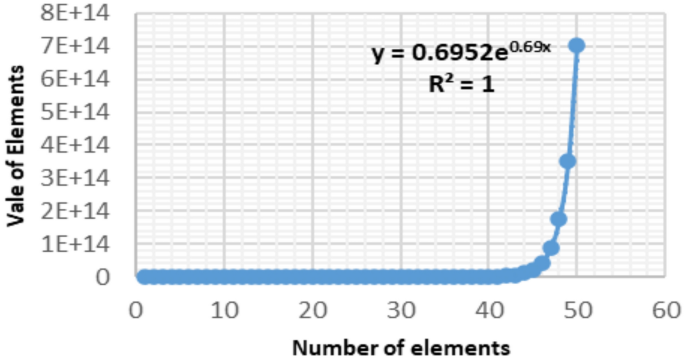
Figure 3 shows the behavior of NS [+ −*] sequence.

Fig. 3
figure 3

Time required to generate the first eight elements of NS (+−*) sequence with 3

Full size image

Sequences formed by a mathematical constraint grow exponentially, are computationally expensive, and involve easy verification procedures.

Properties and numerical trends of NS sequence are reproduced here [40].

Example: Let us consider the first 27 elements in the sequence.

To group all possible permutations, we’ll consider the following scenario:

We have 27 numbers (let’s label them as (N_1, N_2, … N_ 27)). We also have 3 operators (let’s label them as (O_1, O_2, O_3)).

Our goal is to create expressions by combining these numbers and operators. Each expression will consist of one to twenty-seven numbers and three operators. The order of the numbers and operators matters in this case.

Let’s generate some example expressions:

(N_1 + N_2 − N_3 + N_4 + N_5 + N_6…).

We can continue creating such expressions by selecting different combinations of numbers and operators. Since we have 27 numbers and 3 operators, the total number of permutations will be:

Total permutations = 27! ⋅3! = 1,196,790,560.

If the permutations (Order Matters):

If we want to consider all possible arrangements of the 27 numbers (e.g., creating unique sequences), the total number of permutations is:

A staggering 29,142,257,7601.

Algorithm and Complexity of NS [+−*] Series

Definition

NS [+−*] series is a strictly increasing sequence of positive integers, where no element \({{\varvec{E}}}_{\text{n}}\) can be expressed as a combination of additions and/or subtractions and/or multiplications of any subset of the preceding elements \({{\varvec{E}}}_{\text{k}}\) (where \(k<n\)), with each element used at almost once in the combination.

Algorithm

Calculation of the first three elements in the series

Given the initial element \({{\varvec{E}}}_{1}\), a positive integer, then.

$${{\varvec{E}}}_{2}=\left\{\begin{array}{c}{{\varvec{E}}}_{1}+1, \quad {{\varvec{E}}}_{1} !=1\\ {{\varvec{E}}}_{1}+2, \quad {{\varvec{E}}}_{1} =1\end{array}\right.$$

And

$${{\varvec{E}}}_{3}=\left\{\begin{array}{c}{{\varvec{E}}}_{2}+1, \quad {{\varvec{E}}}_{1} !=1\\ {{\varvec{E}}}_{2}+2, \quad {{\varvec{E}}}_{1} =1\end{array}\right.$$

In this way, the 1st 3 elements meet the requirements of the series.

Calculation of the rest of the elements

To obtain \({{\varvec{E}}}_{\text{n}}\), where \(n\) = 4, 5 …

1) Evaluate all expressions formed by any combination of the elements \({{\varvec{E}}}_{\text{k}}\) (where \(0<k<n\)) in the series using the operators + , −, and *.

2) Sort the calculated numbers from the above Step 1) In the ascending order.

3) Find the first calculated number \({{\varvec{N}}}_{\text{f}}\) that meets.

$${{\varvec{N}}}_{\text{f+1}}-{{\varvec{N}}}_{\text{f }}>1$$

And

$${{\varvec{N}}}_{\text{f }}>\boldsymbol{ }{{\varvec{E}}}_{\text{n-1}}$$

4) If \({{\varvec{N}}}_{\text{f}}\) is found, then.

$${{\varvec{E}}}_{\text{n}}={{\varvec{N}}}_{\text{f}}+1$$

Otherwise,

$${{\varvec{E}}}_{\text{n}}=1+\prod_{{\varvec{k}}=1}^{{\varvec{n}}}{{\varvec{E}}}_{{\varvec{k}}}$$

Analysis of Complexity of Algorithm

Evaluation of the Total Number of Expressions

To obtain \({{\varvec{E}}}_{\text{n+1}}\), considering any combination of \(k\) elements (for 0 < \(k<n\)) with the operators + , − , and *, the total number of expressions to be evaluated is.

$${\varvec{N}}={{\varvec{E}}{\varvec{x}}}_{\text{n}}+\sum_{k=2}^{n-1}P\left(n,k\right)*{3}^{k-1}$$

where the 1st part \({{\varvec{E}}{\varvec{x}}}_{\text{n}}\) in the above represents how many expressions can be formed by the exact \(n\) elements with 3 operators [+ , −, *],

$${{\varvec{E}}{\varvec{x}}}_{\text{n}}=n!*{3}^{n-1}$$

and the 2nd part stands for how many expressions are formed by the combinations of any \(k\) elements (\(1<k<n)\) with 3 operators [+ , −, *],

$$\sum_{k=2}^{n-1}P\left(n,k\right)*{3}^{k-1}$$

where \(P\left(n,k\right)\) means choosing any \(k\) elements from \(n{3}^{k-1}\) stands for the number of expressions formed by any combination of the operators [+ , −, *] and one set of \(k\) numbers for 1 < \(k<n\). Based on the definition of \(P\left(n,k\right)\),

$$P\left(n,k\right)=n!/\left(n-k\right)!$$

To derive the element \({{\varvec{E}}}_{\text{n+1}}\) in the series, all expressions formed by any combination of \(k\) elements (for 0 < \(k<n+1)\) paired with the 3 operators must be evaluated.

Computation Complexity

As \(n\) increases, the range of \({\varvec{N}}\) will be estimated below.

Because

$$\text{P}\left(n,\text{k}\right)*{3}^{k-1}= \frac{{{\varvec{E}}{\varvec{x}}}_{\text{n}}}{{3}^{n-k}*(n-k)!}$$

where \(1<k<n\), then

$$\sum_{k=2}^{n-1}P\left(n,k\right)*{3}^{k-1}= {{\varvec{E}}{\varvec{x}}}_{\text{n}}\boldsymbol{*}\left(\frac{1}{3}+\frac{1}{{3}^{2}*2!}+\dots +\frac{1}{{3}^{k}*k!}+\dots +\frac{1}{{3}^{n-2}*\left(n-2\right)!}\right)$$
$${<{\varvec{E}}{\varvec{x}}}_{\text{n}}\boldsymbol{*}\left(\frac{1}{3}+\frac{1}{{3}^{2}}+\dots +\frac{1}{{3}^{k}}+\dots +\frac{1}{{3}^{n-2}}\right)$$
$${={\varvec{E}}{\varvec{x}}}_{\text{n}}\boldsymbol{*}(1-{3}^{2-n})/2$$

As \(n\to \infty ,\) then \(1-{3}^{2-n}\to 1,\) and consequently

$$\sum_{k=2}^{n-1}P\left(n,k\right)*{3}^{k-1}{<{\varvec{E}}{\varvec{x}}}_{\text{n}}/2$$

Therefore, the total number of expressions (\({\varvec{N}}\)) to evaluate is between \({{\varvec{E}}{\varvec{x}}}_{\text{n}}\) and \(3\boldsymbol{*}{{\varvec{E}}{\varvec{x}}}_{\text{n}}/2\), that is,

$${\varvec{n}}!\boldsymbol{*}{3}^{{\varvec{n}}-1}<{\varvec{N}}<{\varvec{n}}!\mathbf{*}{3}^{{\varvec{n}}}/2$$

Sort

The calculated numbers from the expressions are placed into a list that will be sorted using the Python list sort algorithm. The worst-case time complexity (WTC) of this sort of algorithm is bounded above by \({{\varvec{N}}}^{2}\), i.e.,

\(WTC=\) O ([\(n!*{3}^{n}]\)2).

Total Time Complexity (\({\varvec{T}}{\varvec{T}}{\varvec{C}}\))

To calculate an expression with up to \(n\) numbers using additions, subtractions, and/or multiplications, the calculation complexity is O (\(n\)).

The total calculation complexity (TCC) is O (\(n*{\varvec{N}})\). However, TCC becomes negligible compared to WTC.

Therefore, in theory,

\(TTC\approx WTC=\text{O}[ (n!*{3}^{n}]2)\)

Only a small subset of the calculated numbers, derived from the evaluation of all expressions using this adaptive method in the program, is sorted.

Proposed RLP (2:0) Cryptosystem

\(R\hspace{0.17em}=|(N1\hspace{0.17em}+\hspace{0.17em}N2) N3|\hspace{0.17em}+|(N2\hspace{0.17em}+\hspace{0.17em}N3) N1|\hspace{0.17em}+|(N3\hspace{0.17em}+\hspace{0.17em}N1) N2|\)

\(L\hspace{0.17em}=|(N1-N2) N3|\hspace{0.17em}+|(N2-N3) N1|\hspace{0.17em}+|(N2-N1) N2|\)

\(P\hspace{0.17em}=|N1N2|+\hspace{0.17em}N1N3|\hspace{0.17em}+|N2N3|\hspace{0.17em}+|N2N1|\hspace{0.17em}+|N3N2|\hspace{0.17em}+|N3N1|\)

\(RLP (2:0)\hspace{0.17em}=| R*L\hspace{0.17em}+\hspace{0.17em}R*P\hspace{0.17em}+\hspace{0.17em}L*P|+\hspace{0.17em}[R*L*P] |\)

N1 = NS sequence (Add the previous element).

N2 = NS (PM) = NS (+ −) Sequence (Add and subtract previous element).

N3 = NS (PMP) = NS (+ , −, *) Sequence (add, subtract and multiply previous elements).

Handshake Process with RLP (2:0)

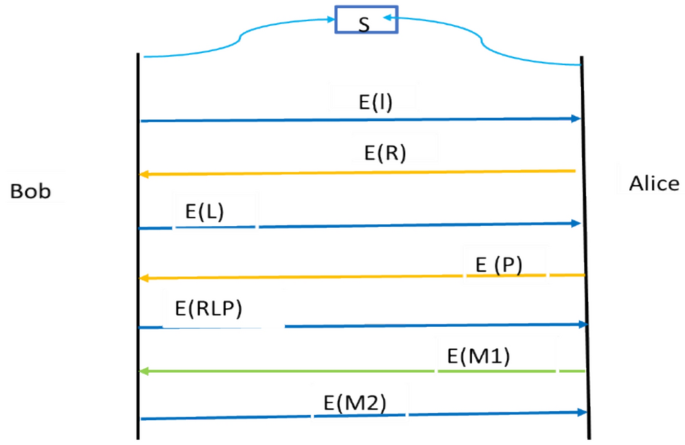
As shown in Fig. 4. Bob and Alice share secret starting value of NS sequence. Bob sends encrypted E(l) value of a random generated length l of sequence using symmetric homomorphic encryption system. Homomorphic encryption enables various mathematical operations on encrypted data without the need for decryption. The operations generally fall into two main categories additive and multiplicative.

Fig. 4
figure 4

Encrypted handshake process with encrypted with symmetric homomorphic encryption

Full size image

Alice computed R value of RLP (2:0) algorithm, and she sent encrypted value of E (R) to Bob, same way Bob sends encrypted value of L E(L) to Alice and Alice responds back with E(P). Thus, both send arithmetically operated values to each other. Then they can decrypt the massage exchange from both parties. If the given point of communication values of R, L and P do not match then communication will be terminated immediately before sending any real message (data).

Enhanced AES with RLP (2:0) [39]

The advanced encryption standard (AES) [10].

Figure 5 shows the 10 steps for regular AES protocol and Fig. 6, illustrate operation in first round of operations.

Fig. 5
figure 5

AES protocol steps

Full size image
Fig. 6
figure 6

AES protocol first cycles (round)

Full size image

The process of generating an NS sequence involves sending and receiving the initial bare 256 binary bits. Binary bits are transformed into decimal numbers (Fig. 7). The first five significant numbers are utilized to generate the stated value of the NS sequence and its length. So, these values are created within the range of 10,000–99999.

Fig. 7
figure 7

AES protocol first cycles with an updated secret key (round)

Full size image

The new secret key generated by the RLP (2:0) algorithm 256 bits value generated by SHA3 has a function.

Security Analysis: Quantum Attack-Resistant Cryptography Discussion

The informal security analysis method is used to discuss the quantum-resistant property of the proposed RLP (2:0) AES encryption mechanism. The proposed cryptosystem focuses on two security aspects and enhances the present AES cryptosystem to make it quantum-attack resistant. These two aspects are discussed as given below [40].

Resistance to Brute Force Attack

One of the most important requirements for the security of any encryption system is the size of the key space. The AES cryptosystem supports three key lengths of 128 bits, 192 bits and 256 bits. This key length size provides huge key space but considering the increasing use of quantum computing, it is advised to integrate more randomness to defend against the quantum brute force attack. One possible threat of quantum brute force is using Grover’s algorithm which is a quantum search algorithm. In the proposed RLP (2:0) cryptosystem, NS sequences are used to create a secret key. The suitability of the NS sequence concerning key space is discussed in Sect. 3.

Enhancing Security in Key Distribution

In symmetric key cryptography, one of the primary security concerns is the exposure of private keys. It is crucial to exercise caution when managing key distribution within a symmetric key framework. Figures 8 and 9 illustrates the updated secret key generation process, which employs two keys: a primary key and a secondary key.

Fig. 8
figure 8

The handshake with NS- sequence for verification of source

Full size image
Fig. 9
figure 9

The single classical/quantum channel architecture

Full size image

The primary key is a random string of bits with a length of either 128 bits, 192 bits, or 256 bits, as supported by the AES cryptosystem. This primary key serves as the symmetric key in a traditional AES setup. To enhance security further, the proposed system incorporates a secondary key derived from no-sum (NS) sequences. In the proposed RLP (2:0) cryptosystem, the secret key can be shared in the same manner as the symmetric key is distributed in conventional AES systems.

Additionally, there is an alternative method for key distribution in the proposed cryptosystem. The same NS sequences can be generated using consistent parameters, such as the starting element, the number of elements in the sequence, period, and amplitude. The primary key can be generated at the source and distributed through traditional means, while the secondary key can be independently generated by both the sender and receiver using the previously agreed-upon parameters. This feature enhances randomness, mitigates the risk of man-in-the-middle attacks, and helps prevent replay attacks.

The NS sequences exhibit characteristics reminiscent of the Knapsack problem, which is a subset-sum problem that involves finding a subset of items that total a specific value. AES systems with large key sizes are still considered quantum safe. Notably, the NS (+−*) sequence, with just 27 elements, offers an astounding 29,142,257,7601 possible combinatorial values.

NS-Enhanced QKD Mechanism

Most of the QKD mechanism uses two channels quantum and classical channels for QKD and still sources remain unverifiable. We propose a reliable technique for verifying the source of QKD transmission. Quantum key distribution is merely one component of the solution. QKD's authentication technique cannot be used to verify the source of the QKD transmission. The NS sequence can solve the problem of verification of the source of quantum key distribution, details of NS (+ −*) sequence are described in [41].

Quantum key distribution is merely one component of the solution. QKD's authentication technique cannot be used to verify the source of the QKD transmission. The NS (+ −*) sequence can solve the problem of verification of the source of quantum key distribution.

As shown in Fig. 8, Bob sends any number N1 of NS (+ −*) sequences and Alice responds with the length (L1) of the sequence and Bob responds back with the starting (S1) value of the sequence. Same way Alice repeats the process by sending 2 and Bob will respond with L2, and Alice will respond by S2. If all parameters match, then they know the source coming from each verified identity. After both side handshakes are verified then only Bob or Alice will share quantum key (QK). If in case of man in middle attack, the parameter will not match at both sides. Also, perimeter values will not match if any of two identities of source or receiver are different. In traditional client–server computing normally we verify the identity of the client; in this scenario we verify the identity of sender and receiver by solving the NS (+ −*) sequence.

The Single Classical/Quantum Channel Architecture

As shown Fig. 9. Quantum channel uses the handshake process shown in Fig. 8, for verification purposes. Once both sender and receiver are verified. The process of quantum key distribution using BB84 protocol. Now Alice encrypts massage using a secrete key generated by quantum channel (QKD) and sends them to Bob over the secure classical channel. Bob uses the same secret key and is able to decrypt massage. The authentication, post process and key shifting and parameter estimation process are handled by classical computer over classical channel.

Conclusions

The research presented in this paper underscores the urgent need for quantum-resistant cryptographic solutions amidst the evolving landscape of quantum computing. By introducing the no-sum (NS) sequence and developing the RLP (2:0) cryptosystem, we demonstrate a viable approach to enhance both symmetric and asymmetric encryption methods, thereby bolstering security against potential quantum attacks. The integration of NS sequences not only improves key generation and distribution processes but also addresses vulnerabilities in existing systems. Furthermore, the application of NS sequences in quantum key distribution (QKD) enhances the verification of parties involved, reinforcing trust in secure communications. As the push for standardizing post-quantum cryptography intensifies, this work contributes valuable insights and methodologies that pave the way for the development of robust cryptographic frameworks capable of withstanding the challenges posed by quantum technologies. Future research we will continue to explore and refine these concepts to ensure the security of data in a post-quantum world.