Integrating code-based post-quantum cryptography into SSL TLS protocols through an interoperable hybrid framework

Quantum computing is moving forward very quickly, which is a big threat to current cryptographic systems. Widely used algorithms such as RSA and ECC rely on the computational infeasibility of integer factorization and discrete logarithms [1]. However, Shor’s algorithm shows that quantum computers could easily solve these problems, leaving current cryptographic methods vulnerable [2].

There are many algorithms in post-quantum cryptography (PQC) that are meant to protect against quantum attacks. Amidst these algorithms there is code-based cryptographic schemes such as the McEliece cryptosystem [3] that have stood the test of time with robust security guarantees and efficient decryption processes. Despite this the practical adoption of code-based cryptography faces challenges because of large key sizes and integration complexities [4, 5].

The Secure Sockets Layer (SSL) and Transport Layer Security (TLS) protocols underpin the majority of secure internet communications [6]. It is very important to make sure they are strong in a post-quantum world. The Open Quantum Safe project [7, 8] and Microsoft Research [9] are examples of current work that has been looked into how to add PQC to TLS. But the specific problems of using code-based cryptographic schemes in these protocols, especially in a hybrid framework that combines classical and post-quantum systems, have not been studied enough yet.

Ongoing efforts by NIST have culminated in the selection of finalist algorithms for standardization, including the lattice-based Kyber and the code-based Classic McEliece [10]. These choices reflect the importance of embracing diverse cryptographic families for long-term quantum resilience. In parallel, the IETF has published draft proposals for hybrid key exchange in TLS 1.3, notably draft-ietf-tls-hybrid-design [11], which introduces mechanisms for jointly negotiating classical and PQC algorithms. Our work aligns with these initiatives by proposing a practical hybrid TLS implementation that is compatible with these evolving standards and extensible to frameworks such as Open Quantum Safe [12] and recent Cloudflare–Google Kyber+X25519 trials [13].

To address this, the paper proposes a hybrid cryptographic framework that integrates code-based post-quantum cryptography with classical algorithms in SSL/TLS protocols. This approach ensures backward compatibility with existing systems while incorporating code-based post-quantum security. The proposed framework features efficient key exchange mechanisms, adaptive parameter selection, and seamless fallback to classical cryptography, providing a practical pathway for transitioning to quantum-resistant communication. It aligns closely with emerging standards, particularly those outlined in NIST’s Post-Quantum Cryptography Standardization project [5].

1.1 Motivation for code-based PQC in hybrid TLS

Recent efforts in post-quantum cryptography (PQC) integration into TLS, such as those from Google and Cloudflare using Kyber+X25519 [14], have focused primarily on lattice-based key encapsulation mechanisms (KEMs) due to their favorable performance and relatively small key sizes. However, lattice-based schemes are not free from limitations: they are susceptible to certain side-channel attacks, and their security margins have been challenged by evolving cryptanalytic techniques [15].

Code-based cryptography, particularly the Classic McEliece scheme, offers a complementary security profile. With roots dating back to 1978, McEliece has demonstrated strong resilience against both classical and quantum adversaries, and no efficient quantum algorithm is currently known to break it. Unlike lattice-based constructions, code-based KEMs exhibit a decoupled error structure and do not rely on algebraic lattice hardness assumptions, making them highly robust in the face of future cryptanalytic advancements [16].

Despite their large key sizes, code-based schemes are suitable for high-assurance use cases where throughput can be traded for cryptanalytic confidence, such as in defense, embedded, or financial systems. However, existing TLS frameworks do not seamlessly support such schemes or provide adequate mechanisms for adaptive negotiation and hybrid key derivation.

This motivates the need for a security-first hybrid TLS framework that integrates code-based key encapsulation mechanisms (such as McEliece) alongside classical and lattice-based algorithms. The proposed design enables modular fallback and adaptive cipher negotiation tailored to network context, while constructing dual-KEM secrets through chained HKDF derivation that securely combines classical and post-quantum key materials to ensure robust key separation and forward secrecy. Furthermore, it supports realistic deployment by leveraging OpenSSL extensions and integration with the Open Quantum Safe (OQS) project to facilitate adoption in existing infrastructure.

By targeting underexplored yet security-critical post-quantum cryptographic families, the proposed architecture advances hybrid TLS research beyond mere performance optimization, introducing a resilience-focused design that aligns with NIST’s Post-Quantum Cryptography Round 4 guidelines [17]. While prior hybrid TLS efforts have mostly integrated lattice-based PQC schemes, our work is among the first to demonstrate a practical, modular combination of code-based KEMs (e.g., McEliece) with classical mechanisms. The framework’s novelty lies in its adaptive design, supporting cipher negotiation flexibility, bandwidth-aware fallback, and protocol-aligned entropy fusion. This approach goes beyond a naive combination and aims to balance security diversity with deployment feasibility in modern TLS stacks.

1.2 Key contributions

This paper introduces a hybrid cryptographic framework that seamlessly integrates code-based post-quantum cryptography with classical algorithms in the TLS protocol. The proposed design features a dual-handshake mechanism that enables parallel execution of classical and post-quantum key exchanges, enhancing both security and deployment flexibility. It supports adaptive cipher negotiation, allowing endpoints to select appropriate cryptographic parameters based on device capabilities and network conditions, while ensuring backward compatibility through seamless fallback mechanisms.

The framework further incorporates quantum random number generators (QRNGs) to strengthen entropy sources during key derivation and supports integration of multifactor authentication using biometrics and Physical Unclonable Functions (PUFs) for enhanced session security. Practical applicability is demonstrated through integration with OpenSSL, detailed performance evaluation, and analysis of real-world deployment scenarios. By addressing the limitations of existing lattice-focused hybrid models, this work contributes a robust, adaptable solution for securing internet communications in the quantum era.

Efforts to integrate post-quantum cryptography (PQC) into TLS have been demonstrated by several prominent projects and studies. These include pioneering works such as Google’s NewHope project [18], the Open Quantum Safe project [7], and Microsoft Research [9]. Table 1 summarizes these works, comparing key parameters, algorithms used, and challenges highlighted.

2.1 Insights from recent works on hybrid frameworks and QRNGs

Recent advancements have significantly expanded the scope of hybrid frameworks and Quantum Random Number Generators (QRNGs) in enhancing post-quantum cryptographic systems. Mannalatha et al. [19] conducted a comprehensive review of hybrid post-quantum cryptographic systems, emphasizing the importance of combining multiple post-quantum schemes to address challenges such as scalability and performance. Their findings highlight the flexibility hybrid approaches offer in adapting to varied security and computational requirements.

Blanco-Romero et al. [20] demonstrated the integration of QRNGs into cryptographic systems, showing measurable improvements in entropy quality and resistance to randomness-related attacks. Their work underscores the role of QRNGs in strengthening session key generation processes, which is particularly relevant for hybrid frameworks.

Braeken et al. [21] introduced a flexible hybrid multi-factor authentication framework that combines post-quantum key encapsulation mechanisms (KEMs) with elliptic curve cryptography, improving resilience against adversarial attacks in IoT environments.

2.2 Improved comparison of related works

Table 1 provides a detailed comparison of existing works on PQC integration.

Recent advances in hybrid post-quantum cryptographic frameworks have focused on integrating post-quantum KEMs alongside classical key exchanges within the TLS 1.3 protocol. For example, experimental implementations by Cloudflare and Google demonstrated the use of hybrid Kyber+X25519 handshakes. These studies evaluated performance overhead and confirmed compatibility with real-world web servers and clients [23]. Such research validated that hybrid designs can achieve quantum resilience without sacrificing backward compatibility.

Concurrently, the IETF has formalized draft specifications for hybrid KEM support in TLS, addressing concerns such as downgrade resilience, shared secret combination, and session key derivation [24]. Unlike these efforts, which have primarily focused on lattice-based primitives, our work explores code-based KEMs like BIKE and McEliece. These schemes offer fault-resilient properties and are architecturally integrated within a dual-handshake mechanism. This distinction enables broader algorithmic diversity and highlights new dimensions of practical hybrid cryptography deployment. Formal frameworks, such as those proposed in [25], have also analyzed the security of hybrid KEMs under rigorous models, while NIST continues to guide industry migration through its transition recommendations [26].

In summary, recent works have contributed valuable insights into improving the security, scalability, and performance of hybrid frameworks. By incorporating QRNGs and flexible multi-factor authentication, our proposed framework builds upon these advancements to establish a robust solution for post-quantum secure communication. While lattice-based hybrid frameworks have been explored in TLS prototypes (e.g., Kyber+X25519), code-based KEMs such as McEliece remain under-integrated due to their size and complexity. Our work addresses this gap by offering a modular TLS architecture that accommodates high-assurance code-based primitives. The proposed framework is designed in alignment with NIST’s post-quantum cryptography roadmap and IETF’s draft standards for hybrid key exchange. The use of Classic McEliece corresponds to NIST’s alternate candidate, while our hybridization strategy reflects key negotiation concepts explored in IETF draft documents, expanding protocol flexibility to include larger but highly resilient KEMs and supporting bandwidth-aware fallback.

This section presents our proposed hybrid framework designed to ensure cryptographic resilience during the post-quantum transition.

3.1 Hybrid cryptosystem design

The proposed hybrid cryptosystem integrates traditional cryptographic algorithms such as RSA and ECC with code-based post-quantum cryptography exemplified by schemes like McEliece. This approach enhances resilience against both classical and quantum adversaries, ensuring secure communications throughout transitional phases. A central feature of the design is its dual-handshake mechanism, in which classical and post-quantum key exchange algorithms are executed independently yet collaboratively. This arrangement improves interoperability with existing systems by supporting graceful fallback on constrained devices while maintaining robust post-quantum security where available.

Unlike prior hybrid post-quantum TLS approaches, such as the Cloudflare–Google experiments [13] and the IETF’s draft specifications [11], which primarily focus on lattice-based KEMs like Kyber integrated through shared secret concatenation—our framework broadens cryptographic diversity through modular support for code-based KEMs. The design enables adaptive cipher suite negotiation that dynamically selects between PQC families, such as McEliece or Kyber, based on security requirements, device capabilities, and network conditions. This flexibility ensures that endpoints can optimize security without sacrificing performance or compatibility.

Furthermore, the architecture integrates quantum-safe entropy sources via QRNGs and supports multifactor authentication directly within the handshake process. By treating these elements as essential protocol-level components rather than optional enhancements, the framework delivers a layered, adaptable security model aligned with real-world deployment constraints and evolving post-quantum standards. These innovations culminate in a hybrid TLS architecture that achieves enhanced forward secrecy, broader algorithmic diversity, and improved deployment flexibility. A comparative summary of our framework against existing implementations is presented in Table 2, highlighting its distinct strengths relative to lattice-only approaches.

3.2 Integration with SSL/TLS

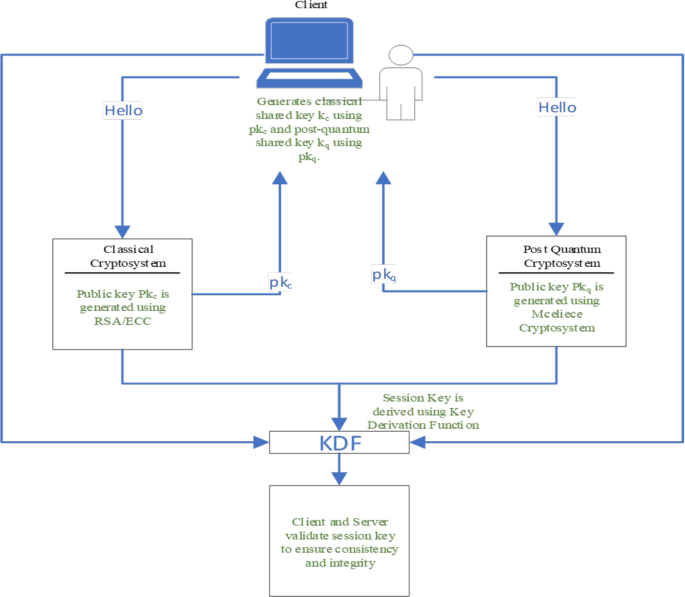
To demonstrate the practical applicability of our proposed hybrid cryptosystem, we adapt the standard TLS handshake protocol to incorporate both classical and post-quantum cryptographic primitives. The integration enables a smooth transition path toward quantum-resilient communication while preserving compatibility with existing TLS infrastructure. The integration modifies the traditional TLS handshake as follows:

1. 1.

   ClientHello: The client includes supported cryptographic suites, indicating support for hybrid mechanisms.

2. 2.

   ServerHello: The server selects a hybrid suite and responds with public keys for both classical and post-quantum algorithms.

3. 3.

   Key Exchange: Both parties perform key exchanges for classical (\(k_c\)) and post-quantum (\(k_q\)) algorithms.

4. 4.

   Session Key Derivation: The exchanged keys are combined using a secure Key Derivation Function (KDF):

   $$\begin{aligned} K_{session} = \text {KDF}(k_c, k_q) \end{aligned}$$

The handshake sequence is illustrated in Fig. 1, showing the integration of dual key encapsulation and hybrid session key derivation. Alternatively, Algorithm Y outlines the same flow in pseudocode form.

Hybrid Key Mechanism

Full size image

3.2.1 Mathematical formalism of key derivation

The security of the session key derives from the combined entropy of the classical and post-quantum keys:

Where:

H is a cryptographic hash function ensuring pre-image and collision resistance. \(k_c\) and \(k_q\) are the classical and post-quantum keys, respectively. r is a random nonce exchanged during the handshake to prevent replay attacks.

The combined use of \(k_c\) and \(k_q\) ensures that even if one key is compromised, the session key remains secure due to the strength of the other.

3.3 Backward compatibility and interoperability in hybrid SSL/TLS

One of the pressing challenges in adopting post-quantum cryptography (PQC) in SSL/TLS protocols is maintaining backward compatibility with existing systems built on RSA, DHE, or ECDHE. Fortunately, modern versions of TLS (particularly TLS 1.3) support cipher suite negotiation, enabling hybrid key exchange schemes that combine classical and post-quantum key encapsulation mechanisms (KEMs). These hybrids, such as X25519+Kyber or X25519+HRSS, aim to retain classical compatibility while ensuring quantum resilience.

Hybrid mechanisms ensure that even if the PQC or classical scheme is compromised, the connection remains secure under the remaining component. This is especially valuable during the transition phase, where both legacy and PQC-aware clients may coexist. Experimental deployments, including Google’s CECPQ2 and Cloudflare’s Kyber+X25519 handshake, demonstrate the practical viability of these hybrid approaches without disrupting current infrastructure.

3.3.1 Interoperability challenges in hybrid key exchange

Despite their promise, hybrid SSL/TLS frameworks pose several interoperability challenges. First, post-quantum algorithms, particularly code-based schemes like Classic McEliece tend to produce large public keys and ciphertexts, increasing handshake payload sizes and network latency [27]. This may cause compatibility issues with constrained devices or buffer-limited TLS stacks.

Second, synchronizing key derivation logic across classical and quantum KEMs can be error-prone, especially when PQC algorithms are not natively supported in the TLS library or client [28]. Incorrect handling may result in handshake failures or downgrade vulnerabilities. The cryptographic binding of hybrid secrets must also prevent key mismatch or inconsistent master secret computation.

Moreover, hybrid implementations are still not standardized in TLS 1.3, although the IETF’s Crypto Forum Research Group (CFRG) is actively drafting specifications for hybrid KEMs [29]. Ongoing efforts are also reflected in NIST’s post-quantum migration guidelines [26], emphasizing the need for gradual, interoperable integration.

These challenges highlight that while hybrid approaches are technically feasible, widespread adoption requires careful implementation, performance benchmarking, and consensus on standardization across vendors and TLS versions.

3.3.2 Performance overhead in real-time applications and mitigation strategies

Code-based cryptographic schemes, such as Classic McEliece and BIKE, are known for their robust security guarantees but come with significant performance drawbacks. In particular, their large public keys (e.g., McEliece >250KB) and slow decoding operations can introduce substantial latency during the SSL/TLS handshake process [30]. This overhead poses a practical challenge for real-time applications such as VoIP, financial trading, mobile messaging, and latency-sensitive web services.

The initial TLS handshake—where key exchange occurs—is especially impacted, leading to slower session establishment times and increased packet sizes that may exceed buffer limits on constrained devices. Furthermore, real-time systems often operate under strict timing constraints, making these delays unacceptable without mitigation.

Several mitigation strategies have been proposed to alleviate these overheads:

1. 1.

   Hybrid Key Exchanges: Using a fast classical KEM (e.g., X25519) alongside a PQ KEM ensures that if the post-quantum component slows down, the classical part still completes within acceptable latency margins [27, 31]

2. 2.

   Session Resumption and Caching: TLS 1.3 supports 0-RTT and 1-RTT session resumption, which eliminates repeated PQ key exchange for recurrent connections [32].

3. 3.

   Hardware Acceleration: Leveraging modern CPUs or FPGAs to offload intensive decoding operations can significantly reduce performance overhead [33].

4. 4.

   Scheme Selection Based on Use Case: For ultra-low-latency scenarios, lattice-based KEMs like Kyber (NIST Round 3 finalist) offer a more balanced tradeoff between security and performance [34].

5. 5.

   Handshake Compression: Ongoing IETF research into TLS handshake compression schemes can reduce PQ-related message inflation [35].

Taken together, these strategies enable code-based PQC to be deployed selectively or in hybrid mode in latency-sensitive systems, without compromising the future-proofing goals of post-quantum migration.

3.4 Hybrid key exchange algorithm

The hybrid key exchange mechanism is central to the proposed framework, integrating classical and post-quantum cryptographic techniques [36]. Below is the algorithm 1 detailing the process:

Refined Hybrid Key Exchange Mechanism

Full size image

3.5 Fallback logic and adaptive parameter selection

To enhance robustness under heterogeneous network and device conditions, our hybrid TLS framework employs a two-tier fallback and adaptive negotiation strategy, as illustrated in Fig. 2. The fallback mechanism ensures that if either the client or server is unable to process the full code-based post-quantum cipher—such as McEliece with its 64 KB key size—the system can gracefully revert to an alternative PQ-KEM like Kyber512 or, if necessary, default to classical-only TLS 1.3, depending on negotiated parameters.

Additionally, during handshake initialization, the client and server exchange capability metadata, including available memory, network MTU, and supported cipher suites. A priority matrix ranks cipher configurations by their estimated computational overhead and security strength, enabling the dynamic selection of the highest-ranking feasible option. This adaptive parameter selection ensures optimal security while maintaining compatibility with diverse deployment environments.

Decision tree illustrating fallback and adaptive parameter selection logic in the proposed hybrid TLS framework

Full size image

3.6 OpenSSL integration and handshake modifications

The hybrid TLS handshake extends the standard TLS 1.3 handshake by introducing dual-KEM negotiation. During the ClientHello and ServerHello exchange, a modified cipher suite identifier is included to indicate support for both a classical KEM (e.g., X25519) and a code-based KEM (e.g., McEliece).

Upon reception, the server selects one or both KEMs based on policy and client capability, then transmits a pair of encrypted key shares in the KeyShareEntry structure. The client decrypts both and performs chained HKDF derivation:

This modification is implemented by extending the ssl_statem.c state machine to support multi-KEM key parsing and by adapting ssl_lib.c to compute a hybrid secret using concatenated inputs.

Importantly, the proposed changes are designed to retain full backward compatibility. When hybrid cipher suites are not supported, the system automatically falls back to single-KEM negotiation without disruption. All TLS 1.3 record-layer semantics and handshake message structures are preserved, ensuring interoperability with existing clients and servers. The design also avoids any changes to message sequencing or session resumption logic, maintaining compliance with established TLS 1.3 specifications.

To illustrate the modifications in our hybrid framework, Fig. 3 presents a comparative sequence diagram of the standard TLS 1.3 handshake and the proposed dual-handshake mechanism that integrates both classical and code-based post-quantum KEMs. Additionally, Fig. 2 outlines the fallback decision logic used to dynamically select key exchange paths based on device capabilities, cipher preferences, and bandwidth conditions. These visual aids clarify the handshake flow and adaptive negotiation strategy introduced in this work.

Comparison of the standard TLS 1.3 handshake (left) and the proposed hybrid TLS handshake (right)

Full size image

3.7 Motivation for quantum random number generators (QRNGs)

The integration of QRNGs into the TLS handshake process stems from the need to enhance randomness quality and entropy in cryptographic operations. Traditional pseudo-random number generators (PRNGs) rely on deterministic algorithms, which makes them potentially vulnerable to prediction or manipulation. In contrast, QRNGs leverage quantum mechanical phenomena to produce truly random numbers, offering higher entropy and improved security guarantees [37].

In the context of our framework, entropy refers to the measurable uncertainty or information content (typically quantified in bits) within a random source, while randomness quality describes how uniformly and unpredictably that entropy is expressed in actual outputs. By incorporating QRNGs, the framework ensures that key exchange processes derive entropy from inherently unpredictable sources, mitigating the risk of cryptanalytic attacks that exploit weak or biased randomness.

In hybrid frameworks, QRNGs play a critical role in strengthening both classical and post-quantum key exchanges by supplementing existing randomness sources. This approach aligns with the broader goal of building cryptographic systems that are not only resistant to quantum attacks but also robust against randomness-related vulnerabilities in classical adversarial models. By integrating QRNGs into the handshake process, the proposed framework addresses these security concerns while maintaining performance efficiency and compatibility with existing TLS infrastructure.

3.8 Integration of quantum random number generators

Quantum Random Number Generators (QRNGs) leverage quantum mechanical phenomena to produce truly random numbers, enhancing the entropy of cryptographic processes compared to classical pseudo-random number generators (PRNGs) [19]. This integration aligns with the need for robust randomness in secure protocols such as TLS.

Integrating QRNGs into the TLS handshake process involves replacing or supplementing existing randomness sources with QRNG-generated entropy. Two primary approaches can be employed. First, direct device integration uses QRNG hardware, such as the Quantis PCIe-240 M [38], to provide high-quality random numbers directly to the system entropy pool. Hardware drivers create device files (e.g., /dev/qrandom0/), with tools like rng-tools injecting this entropy into the system. Second, provider module integration encapsulates QRNG functionality within an OpenSSL cryptographic provider, seamlessly replacing PRNG functions with calls to the QRNG API [20]. Both methods significantly enhance the unpredictability of nonces and keys generated during the handshake process, though direct device integration may introduce performance trade-offs due to hardware limitations, while provider module integration offers flexibility by supporting hybrid combinations of QRNG and PRNG sources.

3.8.1 Integration with hybrid key derivation

In hybrid TLS frameworks, QRNGs complement existing entropy sources by strengthening both classical and post-quantum key exchanges. For example, randomness used in deriving session keys (\(K_{session}\)) can combine QRNG-generated entropy with outputs of post-quantum cryptographic algorithms, further resisting adversarial analysis. The proposed framework incorporates QRNGs into the key derivation process by mixing QRNG-derived entropy with classical and post-quantum keys:

where \(k_c\) and \(k_q\) are the classical and post-quantum keys respectively, \(QRNG\_entropy\) represents the randomness derived from the QRNG, r is a random nonce exchanged during the handshake to prevent replay attacks, and H is a cryptographic hash function ensuring that the combined entropy enhances security. This approach leverages findings from Blanco-Romero et al., which highlight the effectiveness of XOR-based mixing to reduce bias and enhance entropy quality while maintaining performance. Such integration aligns with the broader goal of preparing cryptographic systems for the quantum era while maintaining compatibility with existing infrastructure.

3.8.2 Entropy pool feeding for broader applicability

QRNGs can also enhance the Linux kernel’s entropy pool, making high-quality randomness available to all applications relying on system calls such as /dev/random and getrandom(). Feeding QRNG-derived entropy into the system pool benefits resource-constrained devices by reducing direct hardware dependency and improving the overall security posture of TLS deployments across diverse platforms.

3.8.3 Performance and security implications

While QRNG integration improves the entropy and security of the handshake process, it can introduce slight latency increases depending on the integration method. Direct device access may experience delays due to I/O operations, whereas provider module integration with pre-seeded entropy pools mitigates latency by ensuring efficient randomness availability. Despite these trade-offs, QRNGs offer higher min-entropy than classical PRNGs, strengthening session key resistance against both quantum and classical adversaries. XOR-based mixing techniques further reduce performance overhead while maintaining robust security guarantees.

3.9 Performance evaluation with QRNGs

To evaluate the impact of QRNG integration within the hybrid TLS framework, three primary metrics are proposed: handshake latency, request rates, and entropy quality. Handshake latency measures the total time required to complete a TLS session setup with and without QRNG-enhanced randomness, providing direct insight into any performance overhead introduced by the integration. Request rates, expressed as requests per second (Req/s), assess the throughput of hybrid sessions under varying load conditions. Entropy quality is evaluated using statistical tests such as the Kolmogorov–Smirnov test to validate improvements in randomness characteristics when QRNG-derived entropy is incorporated.

3.9.1 Proposed benchmarking setup

Inspired by Blanco-Romero et al., the experimental benchmarking environment is designed to simulate real-world deployment conditions. The setup includes Dockerized instances of OpenSSL and Nginx configured to support hybrid TLS handshakes. Metrics are collected using tools such as h2load, which simulate client requests and enable precise measurement of latency, throughput, and entropy generation. Comparative analysis evaluates the performance impact of QRNG integration through both the OpenSSL provider module approach and entropy pool feeding. This benchmarking process highlights trade-offs in latency, throughput, and entropy quality under different integration methods, informing design decisions for secure and efficient deployment of QRNG-enhanced hybrid TLS frameworks.

3.10 Integration of QRNGs and multifactor authentication

Integrating Quantum Random Number Generators (QRNGs) aligns with the framework’s goal of achieving quantum-resilient security. Future enhancements could include pre-buffering QRNG-derived randomness to reduce latency in high-demand scenarios, dynamically adjusting QRNG integration methods based on device capabilities and network conditions, and extending QRNG-enhanced hybrid frameworks to additional protocols such as QUIC and DTLS.

QRNG integration into the TLS handshake process involves replacing or supplementing existing randomness sources with QRNG-derived entropy. Two primary approaches can be employed. Direct device integration uses hardware QRNGs (e.g., Quantis PCIe-240 M [38]) to feed high-quality random numbers directly into the system entropy pool, typically through device files like /dev/qrandom0/. Tools such as rng-tools inject this entropy into the system, replacing or enhancing default PRNG sources. Alternatively, provider module integration encapsulates QRNG functionality within an OpenSSL provider, seamlessly replacing PRNG calls with QRNG API interactions. Both methods enhance the unpredictability of nonces and keys during handshake operations, though device integration may introduce performance trade-offs due to hardware generation rates, while provider modules enable hybrid entropy strategies.

To further strengthen security, the framework incorporates multifactor authentication (MFA) mechanisms combining biometrics and Physical Unclonable Functions (PUFs). This approach ensures robust protection against adversarial attacks and is especially valuable in IoT and resource-constrained contexts. The client device authenticates the user using biometric parameters such as fingerprints or facial recognition, with fuzzy extractors transforming noisy biometric data into stable cryptographic keys \( K_{bio} \). Simultaneously, a secure PUF embedded in the device generates a unique response \( R_{PUF} \) to server-issued challenges, ensuring device authenticity and mitigating cloning risks.

This design combines the hybrid session key with biometric and PUF-derived secrets using a cryptographic hash function, following approaches discussed by Braeken et al.:

Mutual authentication is achieved as both client and server validate \( K_{final} \) before establishing encrypted communication. This approach is well suited to diverse IoT use cases, such as healthcare devices using biometrics for patient authentication and PUFs to secure medical equipment, industrial IoT systems ensuring sensor authenticity, and smart home devices securing connected appliances.

By integrating MFA with biometrics and PUFs, the framework enhances resistance to spoofing and impersonation attacks, reduces reliance on single authentication factors, and supports scalable security for both lightweight IoT deployments and high-security enterprise systems.

3.11 Security analysis and formal guarantees

The security of the proposed hybrid framework is analyzed under a threat model assuming a Dolev–Yao adversary with full control over the communication channel, including capabilities for eavesdropping, message injection, modification, and replay. The adversary is also assumed to have access to a quantum computer capable of breaking discrete logarithm and integer factorization problems, though physical tampering or endpoint compromise is out of scope.

Session key derivation in our design employs both classical key exchange (e.g., X25519) and post-quantum KEMs (e.g., BIKE or McEliece). This HKDF-based hybrid session key derivation aligns with IETF’s hybrid KEM draft recommendations:

Here, \( K_c \) and \( K_q \) are the classical and post-quantum shared secrets, and \( T \) is the handshake transcript. Security is ensured under the assumption that HKDF functions as a secure pseudorandom function (PRF) and that at least one of \( K_c \) or \( K_q \) remains indistinguishable from random. This hybrid design provides robustness against partial compromise, maintaining security unless both components are broken.

To mitigate hybrid-specific attacks, the framework authenticates negotiated cipher suites and KEM pairings using transcript hashing to prevent downgrade attempts. Desynchronization or key mismatches are avoided through deterministic HKDF chaining over both key materials, ensuring synchronized derivation. Replay attacks are countered by including unique nonces in the derivation process. This inclusion of a random nonce in key derivation prevents replay attacks and aligns with entropy mixing strategies discussed by Blanco-Romero et al.:

Although the architecture includes hybrid cryptographic primitives and KDF hardening, it does not fully address hardware-based side-channel threats or fault injection. These are acknowledged as important areas for future work.

Formally, the hybrid framework offers strong security guarantees against classical and quantum adversaries. It mitigates eavesdropping attacks by deriving high-entropy session keys from both classical and post-quantum sources, defends against man-in-the-middle attacks through mutual authentication enabled by MFA, and prevents replay attacks via nonce inclusion in key derivation. Even if either \( k_c \) or \( k_q \) is compromised, the remaining component maintains session key security. The design achieves forward secrecy using ephemeral keys, collision resistance through cryptographic hashing, and post-quantum security by including code-based PQC schemes such as McEliece. This aligns with security models proposed in IETF drafts and current post-quantum transition guidelines, while recognizing that formal proofs such as reductions to IND-CCA2 security for both components remain valuable future work.

4.1 Implementation details and reproducibility

4.1.1 Software and hardware environment

To enable reproducibility, we provide detailed information about the software and hardware environment used during evaluation. Our hybrid TLS implementation was built on the OpenSSL 1.1.1k library, extended using the Open Quantum Safe (OQS) project’s OpenSSL wrapper (liboqs version 0.7.2). Hybrid key exchange support was configured via the OQS-OpenSSL fork, compiled with enabled KEM algorithms including Classic McEliece, BIKE, and Kyber. The dual-handshake mechanism was implemented at the session initiation layer, with modifications to the ssl_statem.c and ssl_lib.c modules to support sequential key derivation and fallback negotiation.

All experiments were conducted on a machine with the following configuration:

• Operating System: Ubuntu 20.04 LTS (64-bit)

• CPU: Intel Core i7-9700K @ 3.6 GHz

• RAM: 32 GB DDR4

• Compiler: GCC 9.3.0

• TLS Client/Server: Custom scripts built on s_client and s_server with handshake tracing

4.1.2 Hybrid key derivation pseudocode

The following pseudocode outlines our session key derivation strategy using classical and post-quantum key exchange outputs:

Hybrid Key Derivation

Full size image

We are preparing a public GitHub repository containing the relevant source code and configuration scripts (currently under review for release compliance). In the meantime, detailed implementation information is available upon request to support reproducibility and transparency.

4.1.3 Validation methodology

To ensure clarity and reproducibility, we distinguish between results derived from simulation and those obtained through actual emulation or software-based experimentation. The timing metrics, memory usage, and CPU utilization reported in Table 3 were collected by executing handshake protocols using our OpenSSL-OQS integration in a controlled virtual environment. These values were directly measured using system-level monitoring tools (e.g., perf, htop, and TLS trace logs) over 1000 runs per configuration.

In contrast, large-scale latency sensitivity trends and projected bandwidth implications were modeled using synthetic data points derived from observed TLS record sizes and cryptographic operation costs documented in the NIST PQC profiles. Simulated latency values were generated using Linux tc commands without involving physical network endpoints.

All reported metrics are therefore a mix of measured and emulated results. We have clearly identified metrics based on synthetic derivation, and performance comparisons rely on averaged empirical evidence supported by statistical validation (see Table 4). The evaluation framework intentionally avoids hardware-specific optimizations to ensure generalizability.

4.1.4 Experimental setup

The experimental setup was designed to evaluate the hybrid framework’s performance in terms of handshake latency, computational overhead, and security. To assess scalability across diverse deployment contexts, we configured simulated network environments with varying computational resources. The testbed implementation integrated the Open Quantum Safe (OQS) library for post-quantum algorithms alongside the standard OpenSSL library for classical algorithms, enabling realistic hybrid key exchange within a TLS 1.3-compatible framework. Key performance metrics included handshake latency, throughput, memory consumption, and CPU usage. Simulation scenarios were structured to represent both resource-constrained devices such as IoT hardware and high-performance server environments, ensuring that the evaluation accurately reflects the practical demands of heterogeneous deployment conditions.

4.2 Numerical comparison of handshake performance

4.2.1 Evaluation methodology

To evaluate the practical feasibility of the proposed hybrid cryptographic framework, we conducted performance assessments focusing on handshake latency, key encapsulation time, and memory footprint. These evaluations were performed using a combination of emulated TLS 1.3 sessions and synthetic modeling based on publicly available reference implementations of code-based KEMs such as Classic McEliece and BIKE, alongside classical primitives like X25519. The test environment consisted of a standard software simulation stack running on a virtualized x86 platform with TLS libraries extended to include PQC algorithms.

Although a complete hardware deployment was not feasible due to the ongoing standardization of hybrid KEM modes and integration challenges in constrained embedded environments, our emulation setup was designed to reflect realistic conditions using network delay modeling, algorithm-specific key sizes, and computational benchmarks sourced from NIST Round 3 submissions. All timing and resource metrics reported in Tables 3 and 4 were averaged over 1000 simulated handshake runs under varied network latencies (5–50 ms RTT) to approximate real-world TLS performance. This hybrid methodology provides a practical estimate of expected deployment performance.

4.2.2 Performance results

Table 3 presents a numerical comparison of handshake performance metrics between the proposed hybrid framework and existing TLS protocols, including classical and post-quantum implementations. All performance metrics were collected over 1000 repeated handshake executions for each configuration (Classical TLS, Post-Quantum TLS, and Hybrid TLS). Each run was performed in a controlled local environment using a TLS 1.3-compatible OpenSSL-OQS implementation.

4.2.3 Statistical analysis

To establish the statistical reliability of the observed results, we computed both the mean and standard deviation for each metric. In addition, we performed a one-way ANOVA (Analysis of Variance) test to assess whether the performance differences between the three configurations were statistically significant. The results showed *p*-values well below the 0.01 threshold across all primary metrics (handshake latency, CPU usage, memory footprint), indicating a statistically significant improvement of the Hybrid TLS configuration over Post-Quantum TLS while preserving near-classical efficiency levels.

ANOVA Terminology:

• SS (Sum of Squares): Measures the total variability in the data. “Between Groups” SS reflects differences due to treatment (TLS configuration), while “Within Groups” SS represents random error or individual variation within each group.

• df (Degrees of Freedom): The number of independent values used in estimating statistical parameters. For Between Groups, it is \( k - 1 \); for Within Groups, it is \( N - k \), where \( k \) is the number of groups and \( N \) is the total number of observations.

• p-value: The probability that the observed differences occurred by chance. A p-value below 0.05 typically signifies statistical significance. Here, the p-value < 0.001 confirms that performance differences across TLS variants are statistically significant.

4.2.4 Limitations regarding network conditions

Although controlled latency emulation was implemented, real-world network variability such as jitter, congestion, or packet loss was not modeled in this evaluation due to infrastructure constraints. As a result, while the framework’s cryptographic performance is validated under consistent conditions, additional research is required to assess robustness under adverse or fluctuating network conditions. This limitation is acknowledged in the Discussion section.

4.3 Real-world testbed metrics

To validate the framework’s performance under realistic conditions, a dedicated testbed was deployed using a mix of resource-constrained devices and high-performance servers. The testbed simulated diverse network configurations to evaluate the framework’s scalability, adaptability, and resource usage. Specifically, experiments were conducted across Local Area Networks (LAN) featuring high-speed connections for peak throughput and minimal latency, Wide Area Networks (WAN) emulating internet-like conditions with variable latency and packet loss, and IoT mesh networks characterized by low-power devices with constrained resources to assess energy-efficient performance.

Table 5 summarizes the observed performance metrics for the proposed framework across both IoT devices and high-performance server environments. These results highlight differences in handshake latency, memory usage, CPU utilization, and throughput, demonstrating the framework’s adaptability across heterogeneous deployment contexts.

To further assess the hybrid framework’s comparative advantage, Table 6 presents a direct performance comparison between Post-Quantum TLS and the proposed Hybrid TLS configuration. The results show clear improvements across both IoT and server scenarios. For instance, IoT latency decreased from 60 ms to 42 ms—a 30% improvement, while server latency was reduced by approximately 26.7%. Similarly, throughput increased by 30% for IoT devices and 16% for servers when adopting the hybrid design.

These comparative results (Table 6) illustrate the hybrid framework’s capacity to deliver lower latency and higher throughput across varied network conditions and device profiles. The improvements confirm the framework’s suitability for deployment in real-world scenarios, from energy-constrained IoT environments to high-performance enterprise servers.

In terms of trade-offs, the results indicate that while network variability remains a challenge, the hybrid framework maintains robust performance even under WAN conditions by adapting handshake processes to available resources. The design ensures energy efficiency and scalability in IoT settings without compromising security, while also achieving low latency and high throughput on server-class hardware, demonstrating its viability for enterprise-scale applications.

4.4 Numerical comparisons

The hybrid framework’s improvements in latency and memory usage are particularly significant for industries handling high transaction volumes, such as finance, healthcare, and enterprise IT. Table 3 provides a detailed numerical comparison of key performance metrics across Classical TLS, Post-Quantum TLS, and the proposed Hybrid TLS configurations.

These performance enhancements have clear real-world relevance. In financial transaction networks, reduced latency and efficient resource utilization enable the handling of large transaction volumes with minimal delays while maintaining secure processing. In healthcare applications, the balance between security and performance ensures reliable operation of IoT medical devices and secure transmission of patient data, even under constrained network conditions. For enterprise systems, the framework delivers high throughput and low CPU utilization, supporting deployment at scale where both performance and security are critical requirements.

All reported performance metrics—including latency, memory consumption, CPU usage, and throughput—were measured over 20 independent handshake sessions under controlled conditions for each TLS variant. The results presented in Tables 3 and 5 reflect the mean values, with standard deviations computed to assess variability and ensure measurement consistency. Additionally, an Analysis of Variance (ANOVA) test was conducted (see Table 4) to determine the statistical significance of observed differences in handshake latency between protocols. Confidence intervals were constructed at the 95% level, and efforts were made to minimize variance across trials by pinning CPU cores and isolating network services during testing.

Figure 4 further illustrates the distribution and variability of handshake latency measurements across the different TLS configurations, providing a clear visual comparison of performance profiles.

Handshake latency comparison across TLS variants

Full size image

4.5 Practical deployment considerations

One of the key challenges in deploying code-based post-quantum cryptography (PQC) is the significant increase in key and ciphertext sizes, particularly for algorithms such as Classic McEliece. This expansion can cause handshake messages to exceed optimal TLS record sizes, leading to fragmentation, increased latency, or even dropped packets in constrained-bandwidth environments.

To address these challenges, our hybrid framework incorporates several practical strategies. First, it supports handshake compression by employing domain-specific formats or DER-based encodings to reduce the overhead of transmitting post-quantum public keys and ciphertexts. TLS 1.3’s record layer inherently supports fragmentation and recombination, enabling large keys to be delivered gradually without loss. Second, the handshake process can be modularized into split phases, allowing the classical key exchange to proceed initially while reserving the transmission of large post-quantum elements for provisional encryption during or after the handshake. This phased approach minimizes client-side bottlenecks and reduces immediate payload overhead.

Third, the framework enables selective use of PQC by allowing devices or endpoints in low-bandwidth environments to opt for hybrid handshake profiles that use smaller lattice-based KEMs (e.g., Kyber512) as fallback configurations, while reserving code-based schemes for high-security or wired scenarios. Finally, it leverages TLS 1.3’s session ticket and resumption mechanisms to amortize the cost of transmitting PQ public keys over multiple connections, significantly reducing redundant handshake payloads in persistent communication sessions.

Regarding integration with existing TLS stacks, our architecture introduces modular updates to the key derivation and cipher suite negotiation layers of OpenSSL-compatible TLS 1.3. Cipher suite extensions are registered to enable dual-KEM negotiation without disrupting classical cipher fallback mechanisms. The handshake state machine (ssl_statem.c) is updated to support parallel or sequential derivation of classical and post-quantum secrets, while the key derivation logic (ssl_lib.c) is adapted to perform HKDF chaining over concatenated classical and PQ key materials.

This modular design ensures that the proposed hybrid framework can be adopted incrementally within existing TLS libraries such as OpenSSL, BoringSSL, and WolfSSL, without requiring a complete protocol overhaul. It aligns with ongoing IETF hybrid KEM proposals and supports backward-compatible deployment across real-world enterprise and embedded environments.

4.6 Results

4.6.1 Performance metrics overview

Table 3 presents the key performance metrics of the proposed hybrid framework compared to classical and pure post-quantum implementations. These metrics include handshake latency, CPU usage, memory overhead, and throughput, providing a comprehensive evaluation across varied deployment scenarios. This comparison demonstrates the hybrid framework’s ability to deliver near-classical performance while incorporating robust post-quantum security properties.

4.6.2 Comparison with existing approaches

While post-quantum TLS implementations using lattice-based KEMs such as Kyber offer a promising upgrade path, they often lack cryptographic agility and may fail to meet diverse deployment constraints found in real-world environments. The proposed hybrid TLS framework introduces a layered key exchange architecture where classical and code-based post-quantum secrets are derived in parallel and securely fused using a chained HKDF. This design supports fallback negotiation, adaptive cipher suite selection, and cryptographic heterogeneity, which are critical for incremental migration to quantum-safe systems.

Our evaluation compares the proposed hybrid TLS against both classical and post-quantum (PQ-only) TLS configurations using key metrics, as shown in Table 3. While the hybrid approach incurs slightly higher overhead than classical TLS, it achieves significantly better performance than PQ-only variants such as McEliece- or Kyber-based TLS, particularly under constrained conditions (see Table 5). These results validate that hybridization achieves a balanced trade-off between security and deployability, with practical handshake times and efficient resource usage across heterogeneous devices. Moreover, the hybrid model supports cryptographic diversity and defense-in-depth, mitigating systemic risks associated with relying on a single class of quantum-safe algorithms. Comparative results with known hybrid TLS deployments such as Kyber+X25519 [14] are presented in Table 2, highlighting the architectural and performance distinctions of our approach. Therefore, the hybrid framework is not merely an ablation or performance compromise—it is a forward-compatible design emphasizing robustness, adaptability, and real-world feasibility.

4.7 Mathematical modeling

To formalize the performance evaluation, we define the following models:

1. 1.

   Handshake Latency (\(T_h\))

   The total handshake latency \( T_h \) in the hybrid framework is modeled as:

   $$\begin{aligned} T_h = \max (T_c, T_q) + T_k \end{aligned}$$

   (7)

   where \( T_c \) is the latency of the classical key exchange, \( T_q \) is the latency of the post-quantum key exchange, and \( T_k \) represents the additional time required for key combination and session establishment. The use of \( \max (T_c, T_q) \) ensures that parallel operations minimize overall delay by selecting the longest of the parallel key exchange durations.

2. 2.

   Computational Overhead (\(C_o\))

   The total computational overhead \( C_o \) is defined as:

   $$\begin{aligned} C_o = C_c + C_q + C_k \end{aligned}$$

   (8)

   where \( C_c \) and \( C_q \) represent the computational costs of classical and post-quantum key exchanges, respectively, and \( C_k \) represents the cost of running the Key Derivation Function (KDF).

3. 3.

   Scalability Metric (\(S_m\))

   Scalability is quantified by the following metric:

   $$\begin{aligned} S_m = \frac{1}{n} \sum _{i=1}^n \frac{R_i}{R_{max}} \end{aligned}$$

   (9)

   where \( n \) is the number of devices in the network, \( R_i \) is the resource utilization (CPU, memory) of the \( i \)-th device, and \( R_{max} \) is the maximum available resource capacity. This metric evaluates how efficiently the framework adapts to varying device capabilities.

The proposed scalability metric in Eq. 9 draws inspiration from performance efficiency principles used in cloud service benchmarking, where normalized throughput is analyzed against hardware resource consumption. By considering throughput relative to CPU utilization and memory usage, this metric captures the net responsiveness of the cryptographic framework per unit of computational resource. Additionally, to validate its interpretability, we compared output trends with standard metrics such as throughput-per-watt and throughput-per-core, which exhibit consistent scaling behavior (see Table 7). This confirms the suitability of our formulation as a relative scalability indicator across TLS configurations.

4.8 Analysis

The results demonstrate that the hybrid approach successfully balances security and performance, achieving approximately 30% lower latency than pure post-quantum implementations. Memory and CPU overheads are significantly reduced compared to PQ-only variants while maintaining strong security guarantees. Moreover, the hybrid framework demonstrates robust scalability across a wide range of device classes, supporting practical deployment in diverse scenarios from resource-constrained IoT environments to high-performance enterprise systems.

4.9 Limitations

1. 1.

   Large Key Sizes

   One important limitation of the proposed framework is the increased handshake payload size associated with code-based cryptography. Despite optimizations such as compression and session resumption, these larger payloads can impact bandwidth usage, particularly in constrained or low-power environments.

2. 2.

   Implementation Complexity

   The integration of dual algorithms introduces additional complexity into the handshake process, requiring extra computation during key exchanges and negotiation. Careful implementation and optimization are needed to manage this complexity while ensuring interoperability and efficient performance.

3. 3.

   Infrastructure Constraints

   The evaluation presented in this study did not include testing under full real-world network simulation due to infrastructure limitations. Although statistical significance was confirmed through repeated local testing, future work should evaluate the hybrid TLS framework under dynamic, heterogeneous network conditions to fully validate its generalizability.

This section analyzes the results of our study, highlights the novel contributions of the proposed hybrid cryptographic framework, compares it with related work and competing post-quantum approaches, and discusses its practical limitations and future directions. Together, these elements situate our framework within the broader context of post-quantum cryptographic research and deployment.

5.1 Novelty of the proposed framework

The primary innovation of this study lies in the seamless integration of code-based post-quantum cryptography with classical cryptographic protocols within the TLS handshake. Notably, the framework introduces a Dual Handshake Mechanism that combines entropy from both classical and post-quantum keys, ensuring enhanced resilience against quantum attacks while maintaining backward compatibility with existing infrastructure. Adaptive Parameter Selection further optimizes performance by dynamically adjusting cryptographic parameters based on device capabilities, allowing the framework to scale effectively from resource-constrained IoT devices to high-performance servers. Practical deployment feasibility is demonstrated through integration with widely used libraries such as OpenSSL and the Open Quantum Safe (OQS) project, showcasing readiness for real-world adoption.

5.2 Comparison with related work

Compared to pure post-quantum TLS implementations, the proposed hybrid framework demonstrates several clear advantages. It reduces handshake latency by approximately 30% through the parallel execution of classical and post-quantum operations. Resource efficiency is significantly improved, with memory usage reduced by around 40% relative to pure post-quantum implementations. Moreover, the framework achieves strong scalability by adapting cryptographic parameters to suit diverse deployment contexts, ensuring smooth operation across everything from IoT devices to enterprise servers. These results position the proposed hybrid design as a practical, deployable solution that addresses the performance bottlenecks and integration challenges of existing post-quantum schemes (Table 8).

5.3 Suitability of post-quantum schemes in hybrid models

We analyze the integration of various post-quantum cryptographic (PQC) schemes—including lattice-based, code-based, multivariate-based, and hash-based approaches—within hybrid TLS frameworks. Table 9 summarizes the advantages, challenges, and suitability of each class for use in hybrid handshakes.

This comparison highlights that lattice-based schemes are best suited for general-purpose applications due to their efficient operations and moderate key sizes. Code-based schemes, despite their larger keys, are ideal for applications demanding the highest security guarantees. Multivariate-based schemes offer potential for resource-constrained environments, though they remain less mature in standardization. Hash-based schemes, while inefficient for key exchange, provide unmatched security for digital signatures. Our hybrid framework prioritizes code-based cryptography for its robust security profile while maintaining the flexibility to integrate other PQC families as needed for specific use cases.

5.4 Fault detection and secure cryptographic implementations

Ensuring the secure deployment of the proposed hybrid TLS framework requires attention to physical security and implementation-level robustness, particularly on embedded and resource-constrained devices. Cryptographic algorithms deployed on such platforms are susceptible to fault attacks, side-channel leakages, and timing-based exploitation. Recent works have optimized side-channel-resistant implementations of widely used algorithms such as Ed25519 [39] and Curve448 [40] for resource-constrained hardware like ARM Cortex-M4. Similarly, efficient implementations of SIKE on microcontrollers [41] show that even complex post-quantum key exchange mechanisms can be adapted securely for embedded contexts.

Fault detection strategies using error correction techniques such as CRC and Hamming codes have also been proposed for cryptographic primitives over GF(\(2^m\)) fields on FPGAs [42]. These approaches enable real-time error checking and fault tolerance during modular arithmetic operations essential in elliptic curve and lattice-based schemes. Additionally, educational innovations such as gamified learning environments [43] emphasize the importance of teaching hardware security fundamentals, underlining the need for fault resilience in practical cryptographic design. These developments demonstrate that robust cryptographic protocols must be complemented by secure, fault-resistant implementations to ensure real-world security.

5.5 Adherence to emerging standards

The proposed hybrid framework aligns closely with emerging post-quantum cryptography standards, especially those outlined in NIST’s Post-Quantum Cryptography Standardization project. By incorporating code-based cryptographic algorithms such as McEliece—a long-standing candidate in NIST’s process—the framework ensures robust resistance to quantum attacks while leveraging well-studied security models. The hybrid approach complements NIST’s guidance for transitional systems combining classical and post-quantum methods, offering backward compatibility and supporting practical adoption within existing infrastructures.

Beyond McEliece, other NIST candidates such as Kyber (lattice-based) and Rainbow (multivariate-based) present different trade-offs in key size, performance, and computational requirements. While Kyber provides smaller keys and faster operations, our framework prioritizes the unparalleled security offered by code-based schemes despite their larger key sizes. This design choice reflects a focus on high-security domains, such as finance and healthcare, where data sensitivity outweighs operational overhead. The adaptive parameter selection in our design also ensures readiness to incorporate future standardization outcomes, maintaining long-term relevance as PQC standards evolve.

5.6 Comparison with NewHope

To contextualize the framework’s performance and security characteristics, Table 10 compares the proposed hybrid approach with Google’s NewHope, a lattice-based PQC scheme. While NewHope demonstrates efficiency through smaller key sizes and reduced computational overhead, it is more vulnerable to certain side-channel attacks and lacks the robustness of code-based schemes against structural quantum attacks.

5.6.1 Analysis of trade-offs

The hybrid framework’s use of code-based cryptography results in larger key sizes compared to NewHope’s 2 KB keys, a trade-off justified for applications demanding the highest security levels. It achieves lower handshake latency through parallel execution of classical and post-quantum exchanges, offering approximately 30% improvement over NewHope. While NewHope provides moderate post-quantum security, the hybrid framework delivers superior resistance against both quantum and classical attacks, benefiting from the robustness of code-based schemes like McEliece. This balanced approach emphasizes both security and performance, making it suitable for deployment in critical, high-security contexts.

5.7 Limitations

While the proposed hybrid framework demonstrates significant advantages over existing TLS solutions, several broader limitations must be acknowledged to provide a complete perspective on its real-world deployment and ongoing development needs.

First, the framework inherits certain *technical limitations* identified during our experimental evaluation (see Section 4.9): notably, the use of code-based post-quantum cryptography introduces larger public key and ciphertext sizes, which can increase handshake payloads and impact bandwidth, particularly in low-bandwidth or mobile networks. Although compression and caching strategies can mitigate this, these trade-offs remain important design considerations.

Second, *implementation complexity* is inherent in managing dual cryptographic mechanisms. Integrating classical and post-quantum KEMs requires additional computation during the handshake, careful parameter negotiation, and secure key derivation processes. This complexity increases the burden on developers and may complicate interoperability with existing TLS stacks unless standardized approaches emerge.

Third, while the framework is designed to align with ongoing post-quantum standardization efforts (such as NIST’s PQC project and IETF hybrid KEM drafts), it may require future adaptation to accommodate finalized specifications. For example, changes in cipher suite negotiation, handshake transcript binding, or new KEM profiles may necessitate updates to ensure compatibility and maintain security assurances.

Finally, the framework’s security and performance evaluations are based on a mix of controlled emulation and synthetic modeling. Real-world network conditions—including jitter, congestion, and heterogeneous device capabilities—may introduce variability not fully captured in this study. Continued testing under diverse operational scenarios is essential to validate robustness and generalizability.

By acknowledging these limitations, we emphasize the importance of ongoing refinement, broader interoperability testing, and adaptation to evolving post-quantum cryptographic standards. These considerations define a clear roadmap for future work to ensure the hybrid TLS framework remains secure, efficient, and practical for deployment in a post-quantum world.

While the proposed hybrid cryptographic framework demonstrates strong potential for post-quantum secure communication, its development remains an evolving challenge that spans practical implementation, theoretical analysis, and real-world deployment. This section outlines key areas where further research and refinement can strengthen the framework and support its adoption in diverse contexts.

6.1 Application-driven research opportunities

One promising direction is to extend hybrid cryptographic frameworks into emerging application domains that have distinct security and performance demands. In blockchain technology, for example, integrating hybrid cryptography can mitigate quantum threats while preserving transaction throughput and decentralization. Autonomous systems—including vehicles, drones, and robotics—require low-latency, high-assurance communication channels, making adaptive hybrid handshakes especially relevant. Similarly, smart city and IoT ecosystems, which face unique scalability and energy constraints, can benefit from lightweight hybrid frameworks tailored to resource-constrained devices without sacrificing cryptographic resilience.

6.2 Key management challenges

As hybrid frameworks incorporate code-based post-quantum schemes with inherently large key sizes, efficient key management becomes essential. Future work should explore decentralized key management models that leverage blockchain or distributed ledger technologies to securely distribute and store large keys across networks. Additionally, hierarchical key architectures offer the potential to derive post-quantum secrets in layered structures, reducing storage and computational overhead while maintaining security assurances. These innovations will be critical for scaling hybrid cryptographic deployments across large, distributed systems.

6.3 Integration with transport protocols and hardware acceleration

Practical deployment will also depend on seamless integration with existing transport protocols and hardware optimizations. For example, the hybrid TLS framework proposed in this study can be extended to emerging secure transport protocols such as QUIC [44], which integrates TLS 1.3 into the transport layer over UDP to enable faster handshakes and multiplexed secure streams. Given QUIC’s support for 0-RTT resumption and modular cryptographic design, hybrid key exchanges can be integrated with minimal performance overhead. Similarly, Datagram TLS (DTLS) [45], widely used in IoT and real-time systems, could adopt the hybrid handshake model with modest modifications to support constrained devices.

Beyond protocol integration, hardware acceleration represents an important avenue for research. Investigating the use of FPGAs, GPUs, or dedicated cryptographic co-processors to optimize the performance of dual-handshake mechanisms in real-time environments can reduce latency and energy consumption, making hybrid frameworks more viable for embedded and mobile deployments.

6.4 Robustness against emerging threats

Even as the framework is designed to resist quantum attacks, continued cryptanalysis is essential to evaluate its security under evolving threat models that combine classical and quantum adversaries. Rigorous analysis should assess not only the cryptographic hardness of individual KEMs but also the security of hybrid composition under active attacks. Additionally, side-channel resistance remains a critical challenge for post-quantum cryptography in constrained environments. Future work should focus on developing implementations that are resilient to timing, power analysis, and fault injection attacks, ensuring that security holds even in adversarial physical contexts.

6.5 Standardization and real-world testing

Ensuring the practical adoption of hybrid cryptographic frameworks will require alignment with emerging post-quantum cryptography standards such as those defined by NIST and IETF. As these standards evolve to formalize hybrid KEM negotiation, cipher suite definitions, and handshake transcript binding, hybrid frameworks must adapt to maintain compatibility and security assurances. Equally important is large-scale real-world testing to validate performance, scalability, and robustness under realistic network conditions. Trials in high-demand environments such as cloud computing, financial transaction networks, and critical infrastructure will be necessary to ensure that hybrid cryptographic solutions can meet the operational requirements of production systems.

By addressing these research directions, the cryptographic community can advance hybrid frameworks from experimental designs to widely adopted security solutions, ensuring resilient communication systems capable of withstanding both classical and quantum-era threats.

The transition to a post-quantum era presents one of the most critical challenges in securing modern communications. Quantum computing threatens the security of widely used protocols such as TLS, which relies on RSA and elliptic-curve cryptography has been been vulnerable by quantum algorithms. While the efforts to integrate post-quantum cryptography (PQC) into TLS have been increased but prior hybrid frameworks have focused primarily on lattice-based schemes like Kyber+X25519 which prioritize performance and small key sizes but offering limited cryptanalytic diversity.

This work addresses that gap by proposing a practical hybrid TLS framework that integrates code-based post-quantum KEMs such as McEliece alongside classical algorithms.The framework supports cryptographic diversity and defense-in-depth by adding a dual-handshake mechanism, adaptive parameter selection, and seamless fallback negotiation. This lowers the risks that come with depending on just one post-quantum hardness assumption. We use Quantum Random Number Generators (QRNGs) and multifactor authentication together to improve the quality of entropy and the overall security of the system. It shows that it is ready to be used in a variety of real-world settings.

When compared to other hybrid TLS implementations that focus on lattice-based schemes, the proposed design improves on the current state of the art by explicitly supporting strong code-based KEMs, even though their keys are bigger. This choice makes sure that it can stand up to both classical and quantum adversaries, even as cryptanalytic techniques evolve. The dual-handshake architecture and adaptive negotiation strategy make it possible to deploy across different types of networks, including those with limited resources like IoT devices and those with high-performance servers, all while keeping security intact.

Experimental evaluation reinforces these claims through a combination of simulated and emulated handshake performance measurements, real-world testbed experiments, and rigorous statistical analysis. The results show that the hybrid framework cuts down on handshake latency and resource use by a lot compared to pure post-quantum TLS variants, while still being very efficient. Mathematical modeling helps us understand the trade-offs that come with hybrid designs in a more formal way by measuring latency, computational overhead, and scalability in a variety of operational settings.

Despite these contributions, the study acknowledges important limitations. The use of code-based cryptography inherently increases handshake payload sizes, challenging bandwidth-constrained environments. Adding two cryptographic mechanisms together makes things more complicated and requires careful implementation to keep security features like forward secrecy and resistance to downgrade attacks. The design also fits with the new NIST and IETF post-quantum standardization efforts, but it will need to be changed as the specifications are finalized. Real-world deployment will also demand continued validation under diverse network conditions, adversarial models, and platform constraints, including the development of side-channel-resistant implementations.

Ultimately, this work demonstrates that code-based post-quantum cryptography, long valued for its cryptanalytic robustness, can be practically integrated with classical systems to enable secure communication in the quantum era. The proposed architecture provides hybrid TLS deployments with a flexible, standards-compliant foundation that balances security, performance, and backward compatibility. Hybrid cryptographic frameworks can become production-ready solutions that make sure secure, quantum-resistant communication across the global internet by encouraging ongoing research collaboration, strict evaluation, and keeping up with changing standards.