Multiscale Graph Correlation (MGC)#
With scipy.stats.multiscale_graphcorr, we can test for independence on
high dimensional and nonlinear data. Before we start, let’s import some useful
packages:
>>> import numpy as np
>>> import matplotlib.pyplot as plt; plt.style.use('classic')
>>> from scipy.stats import multiscale_graphcorr
Let’s use a custom plotting function to plot the data relationship:
>>> def mgc_plot(x, y, sim_name, mgc_dict=None, only_viz=False,
... only_mgc=False):
... """Plot sim and MGC-plot"""
... if not only_mgc:
... # simulation
... plt.figure(figsize=(8, 8))
... ax = plt.gca()
... ax.set_title(sim_name + " Simulation", fontsize=20)
... ax.scatter(x, y)
... ax.set_xlabel('X', fontsize=15)
... ax.set_ylabel('Y', fontsize=15)
... ax.axis('equal')
... ax.tick_params(axis="x", labelsize=15)
... ax.tick_params(axis="y", labelsize=15)
... plt.show()
... if not only_viz:
... # local correlation map
... plt.figure(figsize=(8,8))
... ax = plt.gca()
... mgc_map = mgc_dict["mgc_map"]
... # draw heatmap
... ax.set_title("Local Correlation Map", fontsize=20)
... im = ax.imshow(mgc_map, cmap='YlGnBu')
... # colorbar
... cbar = ax.figure.colorbar(im, ax=ax)
... cbar.ax.set_ylabel("", rotation=-90, va="bottom")
... ax.invert_yaxis()
... # Turn spines off and create white grid.
... for edge, spine in ax.spines.items():
... spine.set_visible(False)
... # optimal scale
... opt_scale = mgc_dict["opt_scale"]
... ax.scatter(opt_scale[0], opt_scale[1],
... marker='X', s=200, color='red')
... # other formatting
... ax.tick_params(bottom="off", left="off")
... ax.set_xlabel('#Neighbors for X', fontsize=15)
... ax.set_ylabel('#Neighbors for Y', fontsize=15)
... ax.tick_params(axis="x", labelsize=15)
... ax.tick_params(axis="y", labelsize=15)
... ax.set_xlim(0, 100)
... ax.set_ylim(0, 100)
... plt.show()
Let’s look at some linear data first:
>>> rng = np.random.default_rng()
>>> x = np.linspace(-1, 1, num=100)
>>> y = x + 0.3 * rng.random(x.size)
The simulation relationship can be plotted below:
>>> mgc_plot(x, y, "Linear", only_viz=True)
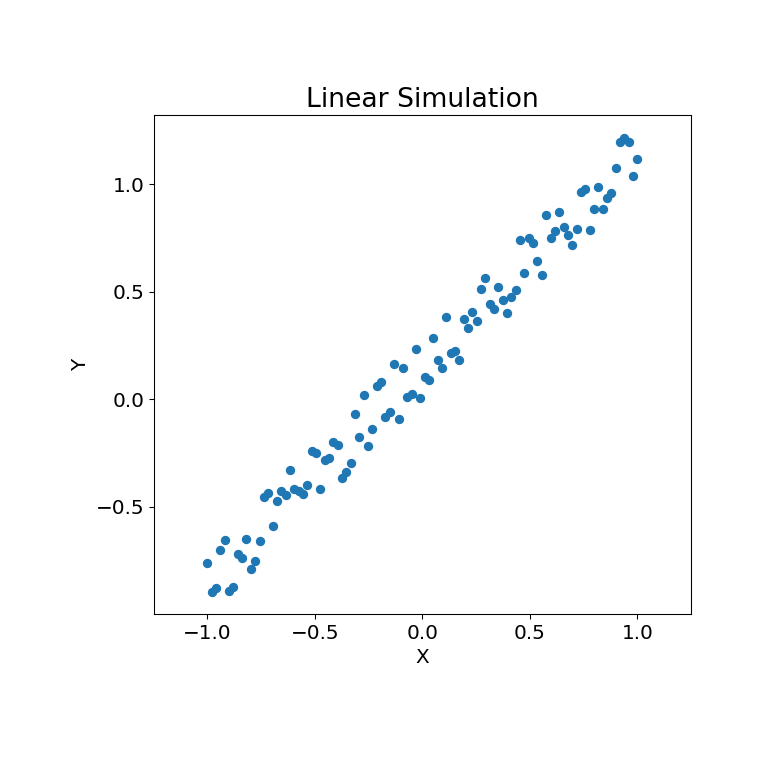
Now, we can see the test statistic, p-value, and MGC map visualized below. The optimal scale is shown on the map as a red “x”:
>>> stat, pvalue, mgc_dict = multiscale_graphcorr(x, y)
>>> print("MGC test statistic: ", round(stat, 1))
MGC test statistic: 1.0
>>> print("P-value: ", round(pvalue, 1))
P-value: 0.0
>>> mgc_plot(x, y, "Linear", mgc_dict, only_mgc=True)
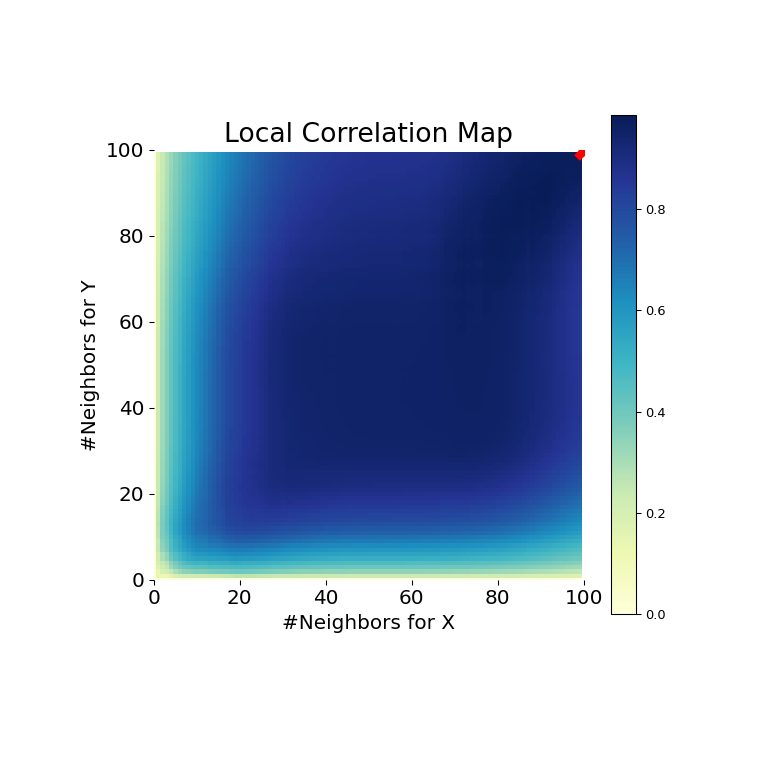
It is clear from here, that MGC is able to determine a relationship between the input data matrices because the p-value is very low and the MGC test statistic is relatively high. The MGC-map indicates a strongly linear relationship. Intuitively, this is because having more neighbors will help in identifying a linear relationship between \(x\) and \(y\). The optimal scale in this case is equivalent to the global scale, marked by a red spot on the map.
The same can be done for nonlinear data sets. The following \(x\) and \(y\) arrays are derived from a nonlinear simulation:
>>> unif = np.array(rng.uniform(0, 5, size=100))
>>> x = unif * np.cos(np.pi * unif)
>>> y = unif * np.sin(np.pi * unif) + 0.4 * rng.random(x.size)
The simulation relationship can be plotted below:
>>> mgc_plot(x, y, "Spiral", only_viz=True)
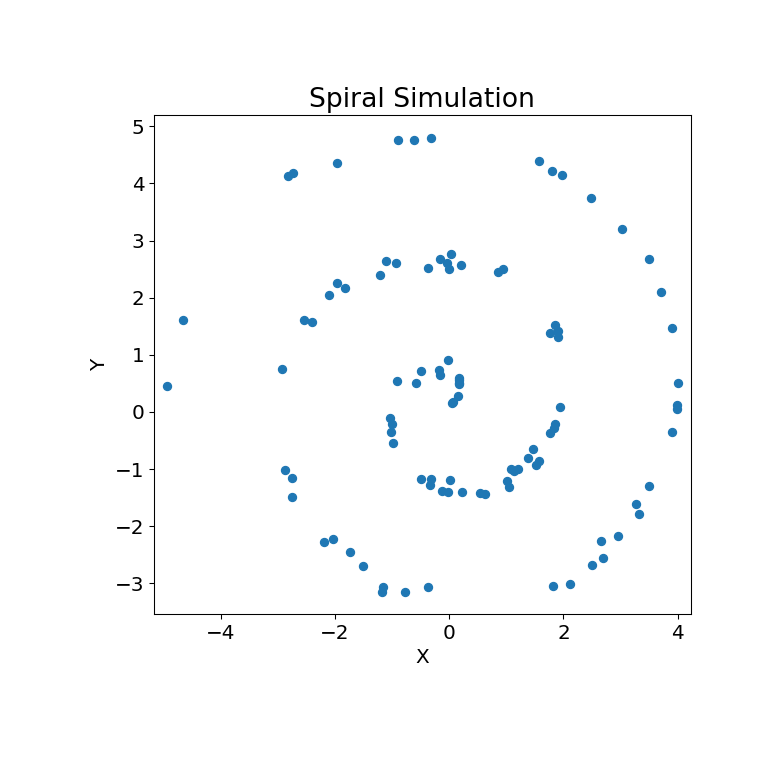
Now, we can see the test statistic, p-value, and MGC map visualized below. The optimal scale is shown on the map as a red “x”:
>>> stat, pvalue, mgc_dict = multiscale_graphcorr(x, y)
>>> print("MGC test statistic: ", round(stat, 1))
MGC test statistic: 0.2 # random
>>> print("P-value: ", round(pvalue, 1))
P-value: 0.0
>>> mgc_plot(x, y, "Spiral", mgc_dict, only_mgc=True)
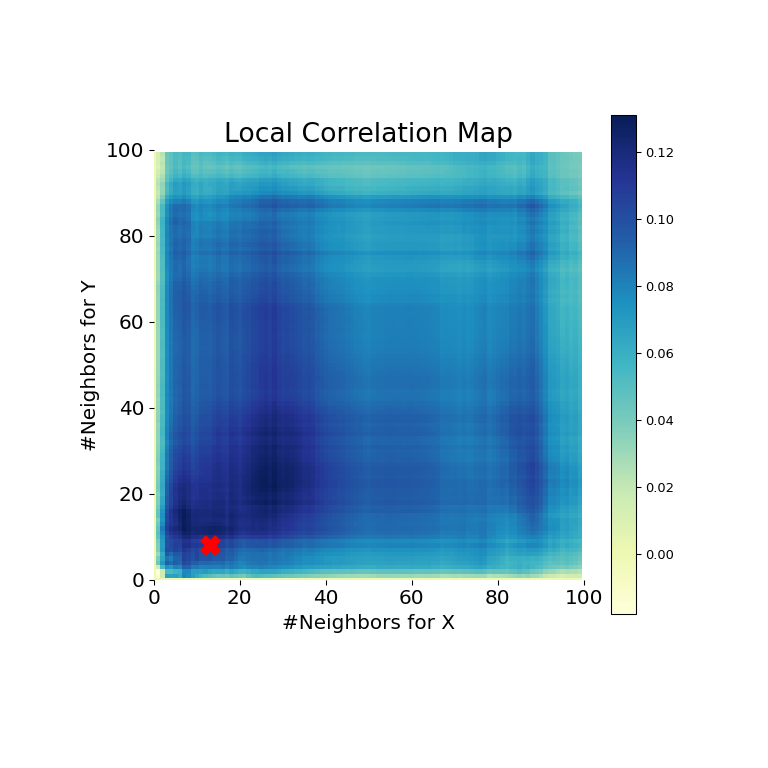
It is clear from here, that MGC is able to determine a relationship again because the p-value is very low and the MGC test statistic is relatively high. The MGC-map indicates a strongly nonlinear relationship. The optimal scale in this case is equivalent to the local scale, marked by a red spot on the map.